두 점 사이의 거리 공식을 이용한 예제 :: 마이구미

"수학을 활용한 예제" 란 카테고리는 한번쯤은 접했던 수학 공식을 활용한 예제를 다룬다.
컴퓨터 비전, 그래픽, 게임 등을 다루지 않으면, 사실 우리가 배운 수학 공식이나 지식을 사용할 일은 많지 않다.
하지만 수학은 프로그래밍에서 확실히 도움이 된다. 
이 카테고리는 수학 공식을 활용하는 예제를 통해 조금이나마 (프로그래밍<=>수학) 연관 관계와 흥미에 도움을 되었으면 한다.
관련 카테고리 링크

 

이 글은 "두 점 사이의 거리"를 활용한 예제를 다룬다.

중학교 때 이미 배웠고, 어렵지 않은 공식이다.

웬만하면 잊어버리지 않는 공식 중 하나일 것이다.

라인스위핑 알고리즘에서도 사용되는 공식이다. (https://mygumi.tistory.com/294)

 

예제를 다루기에 앞서, 이 공식은 어디에서 활용할 수 있을까?

두 점의 거리를 알 수 있다는 것은 많은 경우를 생각할 수 있다.

가장 가까운 두 점, 가장 멀리있는 두 점, 각 점끼리 갖는 거리 등 각 요소들의 거리 관계를 알 수 있다.

이것으로 가장 쉽게 생각할 수 있는 예제는 마우스커서와 가장 가까운 요소를 찾는 것이다.

그렇다면, 우리는 다음과 같은 예제를 만들 수 있다.

 

 

두뇌 게임으로써, 성냥을 옮겨 5개 사각형을 4개 사각형을 만들어야한다.

그 과정에서 미리 가장 가까운 지점을 가이드해주는 용도로 쓰였다.

위 이미지만으로도 충분히 어떻게 활용할 수 있는지 예측할 수 있을 것이다.

 

심플한 버전의 예제를 만들어보자.

마우스 좌표에서 가장 가까운 요소를 포커스하는 예제를 만들어보자.

 

 

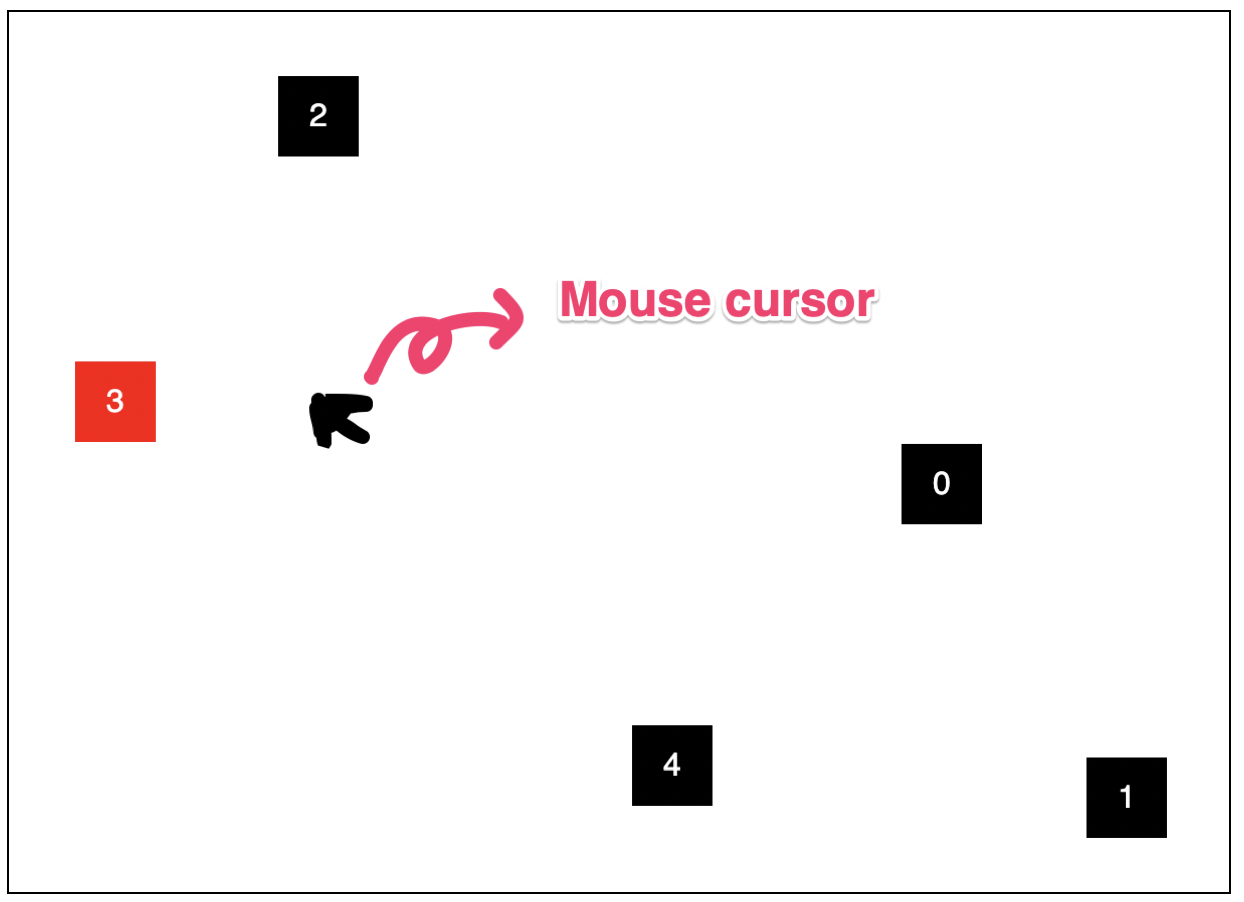
우선 두 점 사이의 거리는 어떻게 구하는가?

아마 공식은 다들 기억할 것이다.

다시 한번 정리해보면 다음과 같다. 

 

 

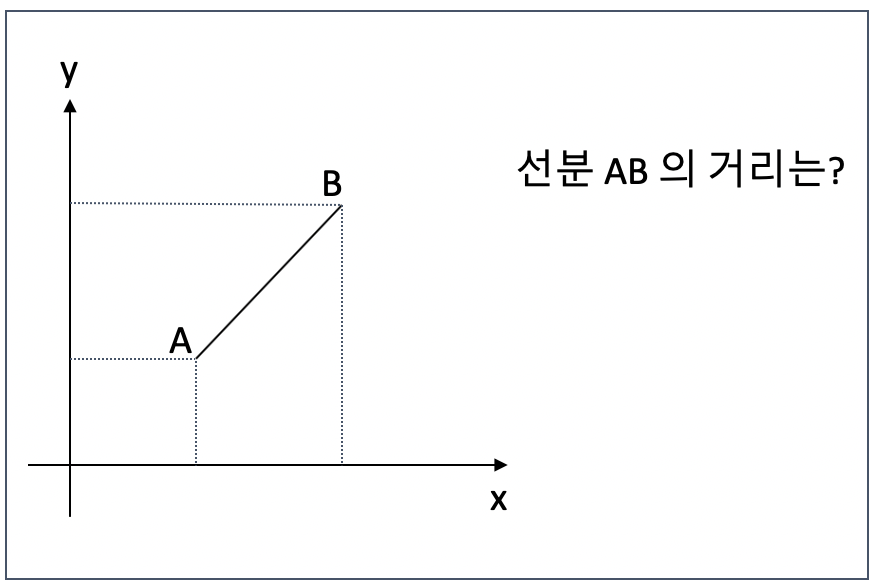
선분 AB 의 길이는 직각삼각형과 피타고라스의 정리를 이용한다.

 

피타고라스의 정리 - 직각 삼각형의 두 직각변를 한 변으로 하는 정사각형의 면적과 같다. 직각 삼각형의 두 직각변 a,b를 각각 한 변으로 하는 정사각형 면적의 합은 빗변 c를 한 변으로 하는 정사각형의 면적과 같다. 이를 피타고라스 정리라고 한다.

 

우선 직각삼각형을 만들면 다음과 같다.

 

 

만들어진 직각삼각형의 빗변 AB 를 구하면 된다.

피타고라스의 정리를 통해 구할 수 있다.

 

 

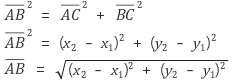
이를 바탕으로, 관련 공식은 굉장히 간단하게 구현할 수 있다.

 

const distance = (cx, cy, mx, my) => {
  return (mx - cx) * (mx - cx) + (my - cy) * (my - cy);
};

 

 

결과적으로 두 점 사이의 거리 공식을 통해 원하는 결과를 구현한 모습을 볼 수 있다.

심플한 코드이기에, 자세한 설명은 생략하고 코드 링크로 대체한다.

이해를 목적을 위해 작성된 코드로써, 코드보다는 전체적인 흐름을 보면 더 도움이 될 것이다.

https://codesandbox.io/s/distance-between-2-points-w2ye2

 

두 점 사이의 거리 공식과 함께 사용한 다른 예

mygumi.tistory.com/387