백준 13415번 정렬 게임 :: 마이구미

이 글은 백준 알고리즘 문제 13415번 "정렬 게임" 을 풀이한다
2016 국민대학교 교내 경시대회 문제이다.
Deque 를 이용하여 문제를 해결하지만, 그 외에도 고려해야하는 것들이 까다로운 문제라고 생각한다.
많은 힌트를 얻었지만, 그래도 까다로운 문제였다.
문제 링크 - https://www.acmicpc.net/problem/13415

 

즐거운 컴퓨터 프로그래밍 시간! 이번 시간의 수업 내용은 정렬이었다. 학생들은 오름차순 또는 내림차순으로 입력받은 값을 정렬해보기 시작하였다. 수업이 끝나갈 무렵, 오늘도 어김없이 조교의 과제가 주어졌다. 과제 이름은 정렬 게임. 과제 내용은 다음과 같다. 처음에 임의의 수열이 있고, 처음 위치부터 지정된 위치까지 오름차순, 내림차순, 오름차순, 내림차순, ... 의 순서를 반복하여 정렬하였을 때, 어떠한 수가 나타나는지 출력하는 프로그램을 작성하는 것이었다.

예를 들어, 과제로 주어진 수열이 [4,1,2,3] 이고, 처음 위치부터 3번째 원소까지 오름차순, 그 다음 2번째 원소까지 내림차순으로 정렬한 결과를 출력하라고 할 경우를 보자. 처음 오름차순 정렬을 수행하면 [1,2,4,3] 이 되고, 여기서 2번째 원소까지 내림차순으로 정렬하면 [2,1,4,3] 이 된다. 그리고 이것이 최종 정답이 된다. 정렬 게임에서 오름차순, 내림차순을 1번씩 하는 것을 한 세트를 진행했다고 정의한다. 수열과 K개의 세트가 주어질 때, 최종 수열을 출력하는 프로그램을 작성하시오.

 

---

 

문제를 이해하기에는 어렵지 않다.

주어지는 범위를 기반으로 오름차순 또는 내림차순으로 정렬을 하면 된다.

하지만 단순히, 주어지는 각 범위를 매번 정렬하기에는 시간초과를 초래한다는 걸 인지할 수 있다.

쉽게 접근할 수 있는 생까은 주어지는 범위 중에서 불필요한 정렬을 최소화하는 것이다.

최소화할 수 있는 부분은 다음과 같다.

 

수열 - 4 1 2 3
정렬 - 2(오름차순) => 3(내림차순)

 

위와 같이 주어졌을 때, 1 ~ 2 번째 요소를 오름차순하고, 1 ~ 3 번째 요소를 내림차순하는 것을 의미한다.

결과적으로, 4 2 1 3 의 결과를 낼 수 있다.

이 부분을 잘 보면, 첫번째 2(오름차순) 을 무시하고, 3(내림차순) 만 동작하면 된다.

즉, 앞의 순서의 값보다 뒤에 오는 값이 크다면, 앞에 있는 정렬은 할 필요가 없다.

예를 들어, 2 -> 3 -> 4.

1 ~ 2 번째 정렬을 하더라도 다음에 1 ~ 3 번째에서도 1 ~ 2 번째를 포함하고 3 번째까지 정렬한다.

그리고 1 ~ 4 번째 정렬도 결국 이전의 요소들을 1, 2, 3 을 포함한 채 정렬하게 된다.

결국 오름차순, 내림차순 상관없이 수만 비교함으로써, 불필요한 정렬을 판단할 수 있다.

 

 

2 3 4 5 6 7 => 7
2 3 4 2 5 4 => 5 4
8 2 4 6 3 2 => 8 6 3 2

 

위처럼 불필요한 정렬의 횟수를 줄일 수 있다.

스택을 통해 이전 값과 현재 값을 비교하면서 위와 필요한 정렬만을 추려낼 수 있다.

하지만 여기서는 추려된 정렬을 순서대로 꺼내야하기 때문에, 큐 같은 성질이 필요하다.

그래서 결과적으로 스택과 큐가 혼합된 deque 를 사용할 것이다.

 

for (int i = 0; i < k; i++) {
    int a = sc.nextInt(); int b = sc.nextInt();
    while (!deque.isEmpty() && deque.getLast().value <= a) {
        deque.removeLast();
    }
    deque.addLast(new Item(a, 1)); // 오름차순 1

    while (!deque.isEmpty() && deque.getLast().value <= b) {
        deque.removeLast();
    }
    deque.addLast(new Item(b, -1)); // 내림차순 -1
}

 

최소환 된 정렬이 있는 deque 에 있는 요소를 뽑으면서 정렬을 하면 원하는 결과를 얻어낼 수 있다.

하지만, 이러한 로직은 시간초과를 초래한다.

불필요한 정렬을 제거하여 횟수를 최소화했지만, 모든 경우를 커버할 순 없다.

주어지는 범위의 수가 100000 -> 99999 -> 99998 -> 99997 ..... 이렇게 주어진다면, deque 에는 주어진 정렬 갯수 그대로가 존재한다.

즉, 불필요한 정렬은 단 한개도 없다.

 

deque 에 존재하는 수들을 생각해보자.

수의 크기를 통해 불필요한 정렬을 걸러내는 작업으로 인해, 결국 deque 안의 요소들은 내림차순으로 존재한다.

그렇다는건, 참고로 Deque 의 첫번째 요소는 가장 큰 수를 의미하고, 정렬에 대한 최대 범위를 의미한다.

결과적으로 배열의 길이가 어떻게되든 첫번째 요소의 수보다 큰 수의 인덱스는 고려하지 않아도 되는 것을 의미한다. (변수 maxIndex 참고)

 

 

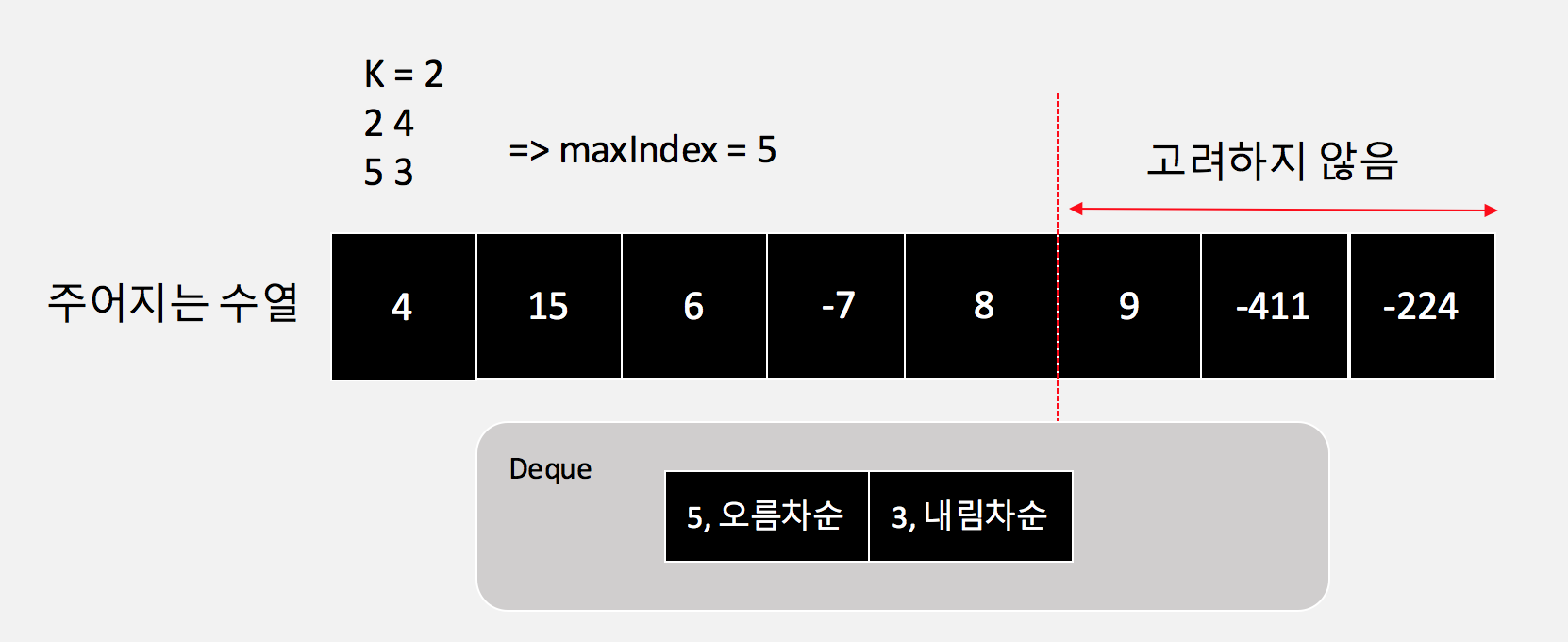
그리고 deque 내부의 요소들에 대해 풀어서 표현하면 다음과 같다.

 

 

이걸 조금 더 고려하면, 우리는 굳이 deque 에서 하나하나 뽑으면서 값에 따라 정렬을 할 필요가 없다는 걸 알 수 있다.

정렬의 범위는 큰수부터 순서대로 온다는 것을 이용해서, 끝에서부터 하나하나 채워간다고 생각하면된다.

 

 

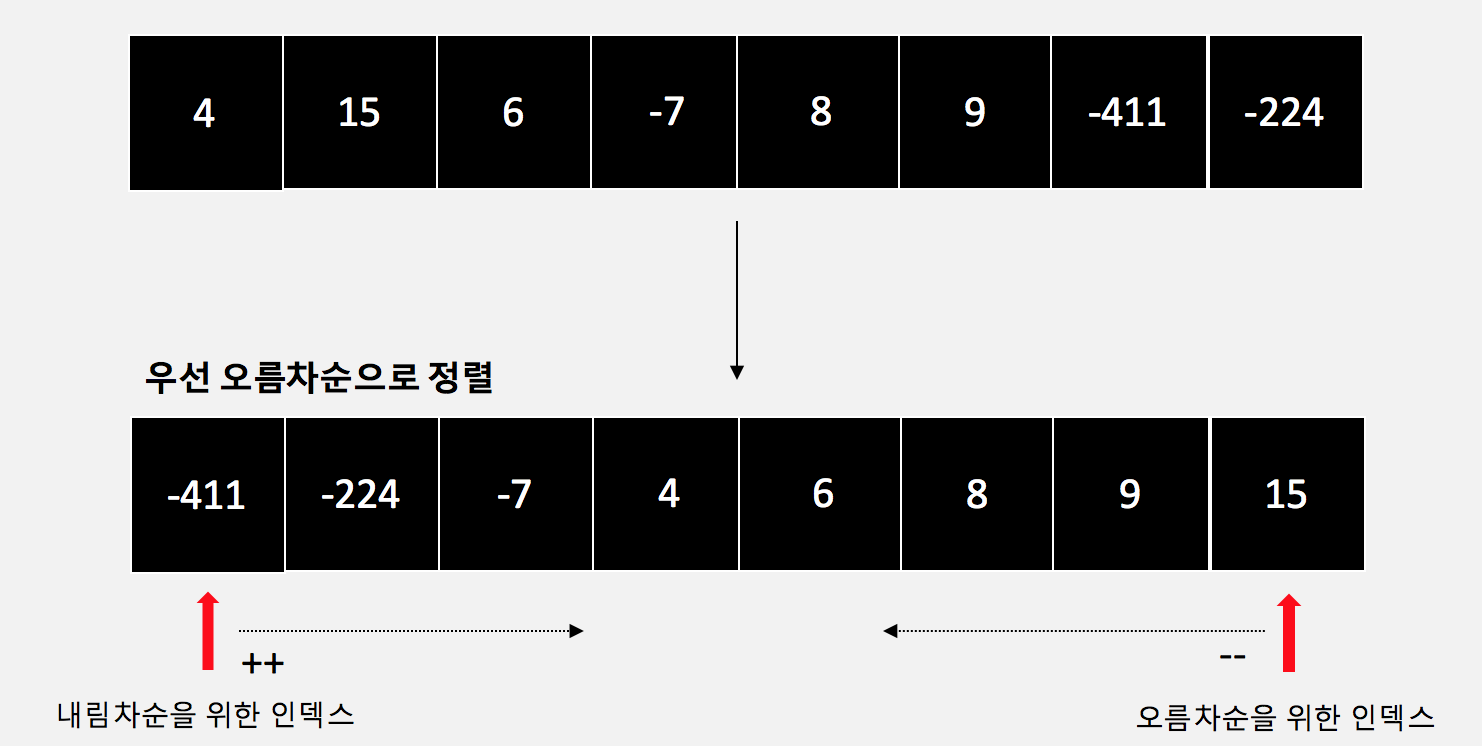
Arrays.sort(array, 1, maxIndex + 1);
while (!deque.isEmpty()) {
    item = deque.removeFirst();
    int start = item.value;
    if (order == 1) {
        for (int i = end; i > start; i--) {
            result[i] = array[ascIndex--];
        }
    } else {
        for (int i = end; i > start; i--) {
            result[i] = array[descIndex++];
        }
    }
    order = item.order;
    end = item.value;
}

 

한번의 정렬을 통해 차순을 맞춰놓은 후, 오름차순과 내림차순을 구분한 인덱스로 증가 또는 감소시키면서 채워나갈 수 있다.

글과 코드를 같이 보는 것이 이해에 더 도움이 되리라 생각한다.

 

Github 전체 코드 - https://github.com/hotehrud/acmicpc/blob/master/algorithm/dequeue/13415.java