비트마스크(BitMask) 는 무엇인가?

알고리즘

비트마스크(BitMask) 는 무엇인가? :: 마이구미

mygumi 2019. 10. 20. 22:40

이 글은 비트마스크(BitMask) 기법에 대해 다룬다.
특정 알고리즘이 아닌, bit 를 활용한 테크닉이라고 할 수 있다.
bit 는 low level 이 아닌 경우에는 크게 비트를 다룰 일은 없어보이지만, 분명 이해가 필요한 경우는 드물지 않다.
그렇기에, 프로그래밍 문제 풀이가 아니더라도 많은 도움이 될 것이다.
대략적인 설명이후에, 백준 알고리즘 2098번 "외판원 순회" 을 풀이한다.
백준 알고리즘 2098번 문제 "외판원 순회" - https://www.acmicpc.net/problem/2098

비트마스크는 무엇인가?

용어 그대로 비트(Bit) 에 관련된 것이다.

비트는 이진 숫자(binary digit) 를 뜻하는 말로 컴퓨터에서 사용되는 데이터의 최소 단위이다.

비트는 0, 1 의 값을 가질 수 있고, true/false 또는 on/off 라는 상태를 나타낸다.

이건 흔히 알고 있는 지식으로 컴퓨터는 0, 1 두가지 숫자만으로 표현하는 이진법을 사용하는 것을 의미한다.

* 일반적으로 우리가 다루는 표현 방식이 0 ~ 9 숫자를 사용하는 10진법이다.

위처럼 이진수 1101 은 우리가 아는 숫자 13로 표현될 수 있다.

비트마스크는 무엇인가?

비트마스크는 이러한 비트의 형태를 활용한다.

알고리즘보다는 테크닉 중 하나로써, 정수의 이진수 표현을 활용한 기법이다.

여기까지 비트를 통해 알 수 있는 2가지 정보는 다음과 같다.

이진수는 0, 1 만을 가지고, true/fasle 상태를 가진다.
이진수는 십진수로 표현 가능하다.

그렇다면 과연 이를 어떻게 활용할 수 있을까?

우리는 길이가 5인 집합 { 0, 1, 2, 3, 4 } 가 존재한다고 가정해본다.

여기서 몇가지 요소를 뽑아 어떤 요소를 선택했는 지 표현할 수 있다.

즉, 집합의 어떤 요소를 구성하고 있는지를 나타내는 부분집합을 어떻게 표현할 수 있는가?

{ 1, 2, 3, 4 }, { 1, 2, 4 }, { 2, 4 }, { 1 } ...........

위와 같은 형태로, Integer 형으로 인덱스를 활용할 수 있다면, 단순히 boolean 배열을 통해 구현할 수도 있다.

int[] array1 = [1, 1, 1, 1, 0];
int[] array2 = [1, 1, 0, 1, 0];
int[] array3 = [1, 0, 1, 0, 0];

하지만 이건 많은 메모리를 차지하고 오버헤드가 증가한다.

비트마스크를 통해 더욱 효율적이게 할 수 있다.

{ 0, 1, 2, 3, 4 } => 11111
{ 1, 2, 3, 4 } => 11110
{ 1, 2, 4 } => 10110
{ 2, 4 } => 10100
{ 1 } => 00010

각 요소는 인덱스처럼 표현할 수 있다.

즉, 집합 i 번째 요소가 부분집합에 존재한다면 1 을 의미하고, 그렇지 않으면 0 을 의미한다.

그리고 위에서 언급했었던, 2진수를 10진수로 표현할 수도 있다.

{ 0, 1, 2, 3, 4 } => 11111 => (2^4 * 1) + (2^3 * 1) + (2^2 * 1) + (2^1 * 1) + (2^0 * 1) = 31
{ 1, 2, 3, 4 } => 11110 => (2^4 * 1) + (2^3 * 1) + (2^2 * 1) + (2^1 * 1) = 30
{ 1, 2, 4 } => 10110 => (2^4 * 1) + (2^2 * 1) + (2^1 * 1) = 22
{ 2, 4 } => 10100 => (2^4 * 1) + (2^2 * 1) = 20
{ 1 } => 00010 => (2^1 * 1) = 2

부분집합을 배열이 아닌 정수를 통해 나타낼 수 있게 된다.

즉, 20 이란 정수는 부분집합 { 2, 4 } 를 나타내는 것을 의미한다.

{ 2, 4 } 부분집합에서 i를 추가하고 싶으면, 단순히 i번째 비트의 값을 1로 변경해주면 된다.

이러한 삽입, 삭제, 조회와 같은 행위는 비트 연산을 통해 쉽게 제어할 수 있다.

제어를 위해 비트 연산에 대해 간략히 설명한다.

AND, OR, XOR, NOT, SHIFT 가 존재한다.

AND 연산(&)

대응하는 두 비트가 모두 1일 때, 1을 반환.

1010 & 1111 = 1010

OR 연산(|)

대응하는 두 비트가 모두 1 또는 하나라도 1일 때, 1을 반환.

1010 | 1111 = 1111

XOR 연산(^)

대응하는 두 비트가 서로 다르면 1을 반환.

1010 | 1111 = 0101

NOT 연산(~)

비트의 값을 반전하여 반환.

~1010 = 0101

시프트(Shift) 연산(>>, <<)

왼쪽 또는 오른쪽으로 비트를 옮긴다.

00001010 << 2 = 101000
00001010 >> 2 = 000010

왼쪽 시프트는 A * 2^B 를 의미하고, 오른쪽 시프트는 A / 2^B 를 의미한다.

0001 -> 0010 -> 0100 -> 1000 => 1, 2, 4, 8 .....

1000 -> 0100 -> 0010 -> 0001 => 8, 4, 2, 1 .....

(A + B) / 2 를 (A + B) >> 1 로 사용할 수도 있듯이 많은 곳에서 일반적인 사칙연산을 더 효율적으로 할 수 있다.

기본적인 비트 연산을 연습할 수 있는 문제를 통해 해보는 것도 나쁘지 않다. (https://www.acmicpc.net/problem/12813)

비트 연산자를 사용해도 되지만, 이론적으로 구현하면 다음과 같다.

// A&B
for (int i = 0; i < len; i++) {
    c[i] = a[i] == 1 && b[i] == 1 ? 1 : 0;
}
// A|B
for (int i = 0; i < len; i++) {
    c[i] = a[i] == 1 || b[i] == 1 ? 1 : 0;
}
// A^B
for (int i = 0; i < len; i++) {
    c[i] = a[i] != b[i] ? 1 : 0;
}
// ~A
for (int i = 0; i < len; i++) {
    c[i] = a[i] == 1 ? 0 : 1;
}
// ~B
for (int i = 0; i < len; i++) {
    c[i] = b[i] == 1 ? 0 : 1;
}

이제 어떻게 비트 연산을 통해 삽입, 삭제, 조회를 할 수 있는가?

1010 로 표현하고 있을 때, i번째 비트의 값을 1로 어떻게 변경할 수 있을까?

i = 2 이라고 가정할 때, 결과는 1110 을 원한다.

2번째 비트를 1로 변경할 수 있는 방법은 다음과 같다.

1010 | 1 << 2
1010 | 0100 => 1110

시프트 연산을 통해 2번째 비트만 1로 할당되어 있는 이진수를 만든다.

그리고 OR 연산을 통해 원하는 결과를 만들 수 있다.

반대로 2 번째 비트의 값을 0로 어떻게 변경할 수 있을까?

1110 & ~1 << 2
1110 & 1011 => 1010

AND 연산과 NOT 연산을 활용할 수 있다.

그리고 i번째 비트의 값을 알 수 있는 방법은 다음과 같다.

A & (1 << i)
2번째 비트 - 1010 & (1 << 2) = 1010 & 0100 => 0
3번째 비트 - 1010 & (1 << 3) = 1010 & 1000 => 1000

AND 연산과 시프트 연산을 통해 i번째 비트의 값이 0이라면 값이 0이라는 것을 알 수 있다.

이렇게 비트를 활용한 테크닉을 통해 접근하는 것이 비트마스크인 것이다.

마지막으로 문제를 통해 비트마스크를 활용한 예를 보자.

비트마스크를 대표 문제라고도 볼 수 있는 "외판원 순회"이다.

이 문제의 풀이는 사실상 동적계획법(DP)에 비트마스크를 접목한 방식이다.

외판원 순회 문제는 영어로 Traveling Salesman problem (TSP) 라고 불리는 문제로 computer science 분야에서 가장 중요하게 취급되는 문제 중 하나이다. 여러 가지 변종 문제가 있으나, 여기서는 가장 일반적인 형태의 문제를 살펴보자.
1번부터 N번까지 번호가 매겨져 있는 도시들이 있고, 도시들 사이에는 길이 있다. (길이 없을 수도 있다) 이제 한 외판원이 어느 한 도시에서 출발해 N개의 도시를 모두 거쳐 다시 원래의 도시로 돌아오는 순회 여행 경로를 계획하려고 한다. 단, 한 번 갔던 도시로는 다시 갈 수 없다. (맨 마지막에 여행을 출발했던 도시로 돌아오는 것은 예외) 이런 여행 경로는 여러 가지가 있을 수 있는데, 가장 적은 비용을 들이는 여행 계획을 세우고자 한다.
각 도시간에 이동하는데 드는 비용은 행렬 W[i][j]형태로 주어진다. W[i][j]는 도시 i에서 도시 j로 가기 위한 비용을 나타낸다. 비용은 대칭적이지 않다. 즉, W[i][j] 는 W[j][i]와 다를 수 있다. 모든 도시간의 비용은 양의 정수이다. W[i][i]는 항상 0이다. 경우에 따라서 도시 i에서 도시 j로 갈 수 없는 경우도 있으며 이럴 경우 W[i][j]=0이라고 하자.
N과 비용 행렬이 주어졌을 때, 가장 적은 비용을 들이는 외판원의 순회 여행 경로를 구하는 프로그램을 작성하시오.

모든 도시를 한번만 방문하면서 다시 시작점으로 돌아오는 최소 거리 비용을 구하는 문제이다.

이 문제는 완전탐색 문제로써, 단순하게 풀면 경우의 수가 N! 로 시간초과를 경험하게 된다.

시간을 줄이기 위해 동적계획법으로 접근하고, 점화식은 다음과 같다.

dp[current][visited] = min(dp[current][visited], tsp(next, visited + next) + w[current][next])

현재 도시가 current 이고, 방문한 도시들의 집합이 visited 일 때, 나머지 도시들을 순회한 최소 비용이다.

여기서 visited 를 배열로 관리하는 것이 어렵기에, 비트마스크를 활용하는 것이다.

도시이 0~3번 까지 존재할 경우, 0번, 3번 도시를 들렸다는 것은 1001 로 표현할 수 있고, 정수로는 9를 의미한다.

즉, 2번 도시에서 0번, 3번을 방문하고 순회했을 때의 최소 비용은 dp[2][9] 를 의미하는 것이다.

점화식 이해를 위해 그림으로 조금 설명을 덧붙인다.

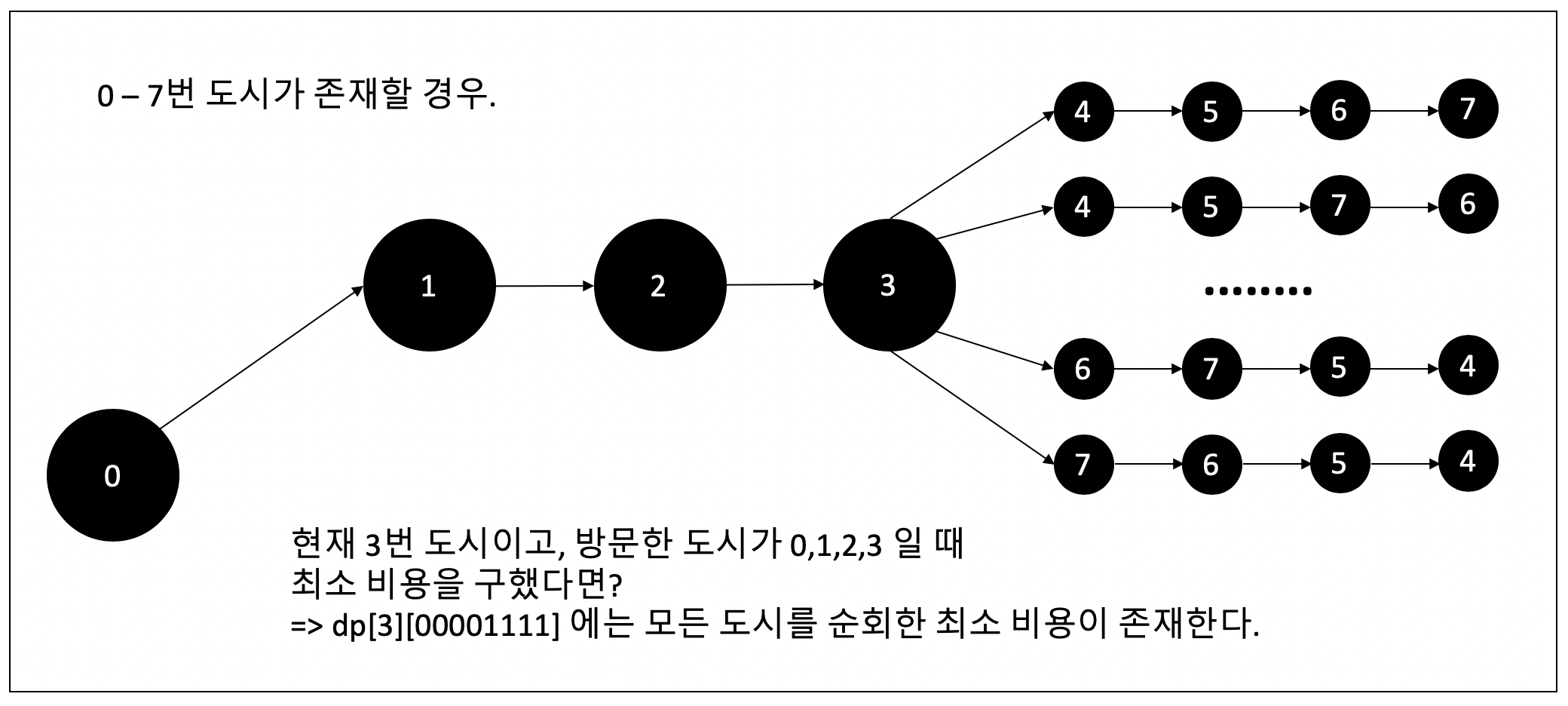
위처럼 dp[3][00001111] 에 모든 도시를 순회한 최소 비용이 구했다고 가정한다.

그렇다면, dp[3][00001111] 에 해당되는 것들은 나머지 도시들을 방문하지 않고, 이 최소 비용을 재사용하면 된다.

여기서 dp[3][00001111] 가 해당하는 경로는 다음과 같다.

0 -> 1 -> 2 -> 3 -> .......
0 -> 2 -> 1 -> 3 -> .......
0 -> 3 -> 1 -> 2 -> .......
0 -> 3 -> 2 -> 1 -> .......

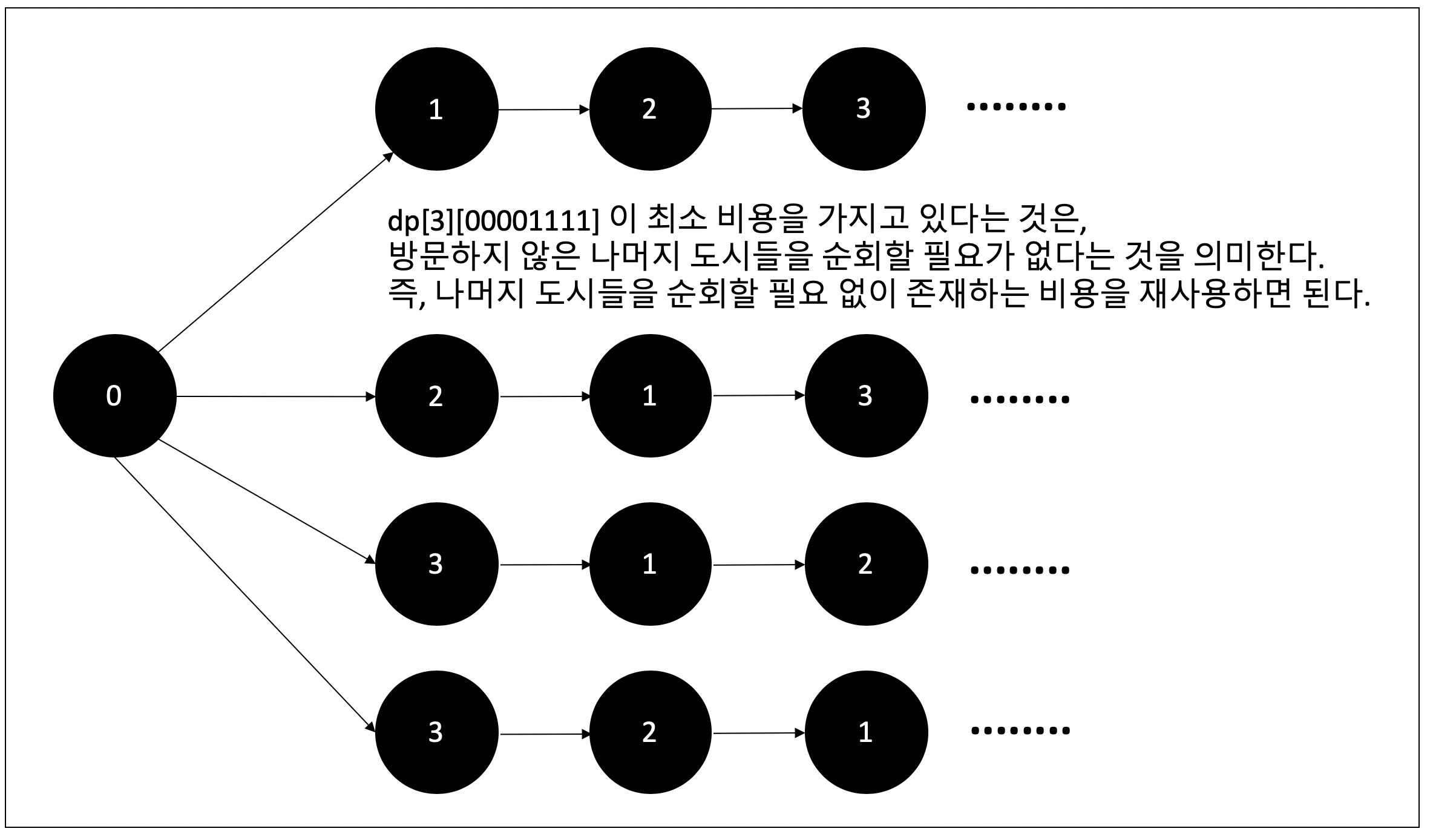
위와 같은 부분적으로 문제를 나누어 해결한 모습을 볼 수 있다.

여기서는 사용되는 비트 연산은 다음과 같다.

모든 도시를 방문한 경우. (모든 비트의 값이 1 인지 판단)
이미 방문한 도시 여부. (i번째 비트의 값이 1 인지 판단)
다음 도시를 방문했을 경우. (i번째 비트의 값을 1로 변경)

자세한 건 전체 코드를 참고하길 바란다.

비트마스크 자체는 어려울 게 없으나, 다른 알고리즘 함께 사용되어 어렵게 느껴질 수 있다.

제약이 있지만, 여러모로 유용하게 쓸 수 있는 테크닉이라고 볼 수 있다.

백준 2098번 외판원 순회 전체 코드 - https://github.com/hotehrud/acmicpc/blob/master/algorithm/bitmask/2098.java